Reflexión y Transmisión de ondas en cuerdas

Reflexión y transmisión de ondas en cuerdas

Fundamento teórico

I. INTRODUCCIÓN

Supongamos
                   una onda
                  armónica de frecuencia f (pulsación w =
                  2pf) que se propaga sobre la
                  cuerda 1, e
                  incide sobre la unión a otra cuerda 2 de diferentes
                  características. La tensión T aplicada sobre ambas cuerdas
                  es la misma. Las densidades lineales de masa en ambas cuerdas
                  son, respectivamente  m₁ y m₂. Sabemos que las velocidades
                  de propagación
                  de la onda serán C₁=Ö(T/m₁) para la cuerda 1 y C₂=Ö(T/m₂) para la cuerda 2.
                  Puesto que la frecuencia no se modifica (el punto de contacto
                  en ambas cuerdas
                  las mantiene unidas en todo momento) la longitud
                  de onda será diferente en cada una de las cuerdas. Tales
                  longitudes de onda serán,
                respectivamente, λ₁ = C₁/f y λ₂ = C₂/f.

II. FUNDAMENTO TEÓRICO

II.a. Reflexión y trasmisión de ondas armónicas

· Comenzamos escribiendo la solución armónica para la onda incidente en el medio 1:

;

donde es su amplitud y

· Al llegar al punto de unión entre ambas cuerdas (x=0), parte de dicha onda se reflejará al medio 1 y parte de la onda se trasmitirá al medio 2. La expresión de dichas ondas será:

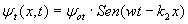
donde

· Las condiciones de frontera en la unión (x=0) nos permiten hallar las relaciones y .

A tales coeficientes les llamaremos, respectivamente, coeficientes de reflexión y trasmisión de amplitud de desplazamiento.

· Resultan evidentes las dos condiciones de frontera que han de cumplirse en el punto de unión (x=0).

El desplazamiento del punto x=0 ha de ser idéntico evaluado desde la cuerda 1 y desde la cuerda 2, si ambas cuerdas han de seguir en contacto en dicho punto,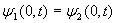

y puesto que la onda en el medio 1 es la suma de la incidente y de la reflejada,

, por tanto

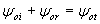
Por otra parte, las fuerzas verticales ejercidas desde cada cuerda sobre el punto de unión deben ser iguales y opuestas pues, en caso contrario, un elemento diferencial de masa en dicho contacto adquiriría una aceleración infinita.

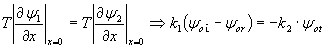
como podemos escribir la última ecuación como,

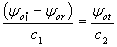· Resolviendo las ecuaciones obtenidas:

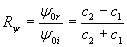
· Podemos escribir tales coeficientes en función de diferentes variables:

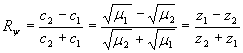
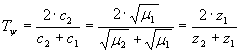
donde y son las impedancias mecánicas características de ambas cuerdas.

II.b. Reflexión y trasmisión de pulsos

· La expresión matemática para un pulso o forma de onda arbitraria es más compleja que para el caso de ondas armónicas, las cuales requieren, en rigor, ser de extensión infinita. La solución (por el método de D'Alembert) para la ecuación de ondas en una dimensión resulta ser una función arbitraria f(x - ct), si consideramos desplazamiento hacia la derecha.

La solución de la ecuación de onda puede escribirse en la forma:

en lugar de la habitual

De esta forma, podemos representar la perturbación incidente como: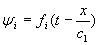

· Las perturbaciones reflejada y trasmitida podremos ponerlas, asimismo, como funciones arbitrarias en sus variables adecuadas:

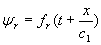
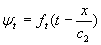
· Las condiciones de frontera siguen siendo análogas:

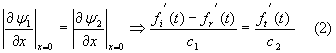
· La integración de la ultima ecuación nos lleva a:

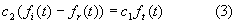
· Resolviendo (1) y (3) obtenemos:

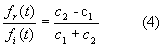
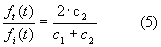
· Podría pensarse que las relaciones halladas son únicamente válidas en la posición x = 0. Este es el resultado encontrado, pero también es cierto que tales relaciones son válidas también en x = 0 para todos los instantes de tiempo mientras sucede la incidencia del pulso. Por consiguiente, la relación que verifican los pulsos reflejado y trasmitido (respecto del incidente) en un instante para x = 0, se verificará en un instante posterior para las nuevas posiciones que ocupen en sus correspondientes medios (medio 1 para la reflejada y medio 2 para la trasmitida), según sus velocidades de propagación.

· De esta forma, transcurrido un tras la llegada del pulso incidente al punto que separa los medios, el valor del desplazamiento de la onda reflejada en el punto x = - c será el valor que tomaría la incidente si siguiese su camino en el medio 2, por el coeficiente hallado en la ecuación (4)

.

· Idéntico razonamiento se puede aplicar para la onda trasmitida, pero teniendo en cuanta que en el medio 2 la velocidad de propagación es C₂, con lo que para la trasmitida. En definitiva: