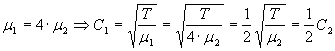SITUACIÓN A

SITUACIÓN B

·        CONSIDERAREMOS DOS CASOS. En el primero de ellos (a), la cuerda 1 es de cuádruple densidad lineal másica que la cuerda 2, es decir, m₁ = 4m₂. En el segundo caso (b), la cuerda 2 posee una densidad lineal másica cuádruplo que la correspondiente a la cuerda 1, es decir, m₁ = m₂/4.

·        Situación a)

Así pues, tanto la longitud de onda como la velocidad de propagación en el medio 2 duplican los valores correspondientes del medio 1.

·        Utilizando los coeficientes de reflexión y trasmisión de amplitud de desplazamiento mostrados en el fundamento teórico para ondas armónicas.

 y

 

 

 

 

 

 

 

 

·        Situación b) 

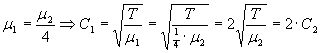
Así pues, tanto la longitud de onda como la velocidad de propagación en el medio 1 duplican los valores correspondientes del medio 2.

·        Utilizando los coeficientes de reflexión y trasmisión de amplitud de desplazamiento mostrados en el fundamento teórico para ondas armónicas.

 y

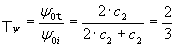
·        Estas situaciones se muestran claramente en las animaciones presentadas.

 

En el dibujo m representa la masa de la cuerda 2.

·        CONSIDERAREMOS DOS NUEVOS CASOS. Surgen como casos extremos en la reflexión y trasmisión de ondas armónicas.

·       Situación c) Si consideramos que la densidad lineal de masa de la segunda cuerda es infinita, podemos denominar a esta situación como de extremo fijo, ya que a efectos prácticos es como si la cuerda estuviese atada en su extremo a un punto fijo. En las ecuaciones anteriores resulta inmediato deducir el coeficiente de reflexión de amplitud de desplazamiento:  según esto, la onda reflejada posee la misma amplitud que la incidente pero invertida, es decir, desfasada π. . Por supuesto, no existe onda transmitida.

 

En esta figura la cuerda se encuentra anclada en su extremo derecho.

 

 

 

 

 

 

 

·       Situación d) Si consideramos que la densidad lineal de masa de la segunda cuerda es cero, podemos denominar a esta situación como de extremo libre, ya que a efectos prácticos es como si la cuerda estuviese libre en su extremo derecho. En las ecuaciones anteriores resulta inmediato deducir el coeficiente de reflexión de amplitud de desplazamiento: la onda reflejada posee la misma amplitud que la incidente y en fase. Por supuesto, no existe onda transmitida.

 

En esta figura la cuerda se encuentra libre en su extremo derecho, desliza sobre la barra.

 

 

SITUACIÓN C

SITUACIÓN D